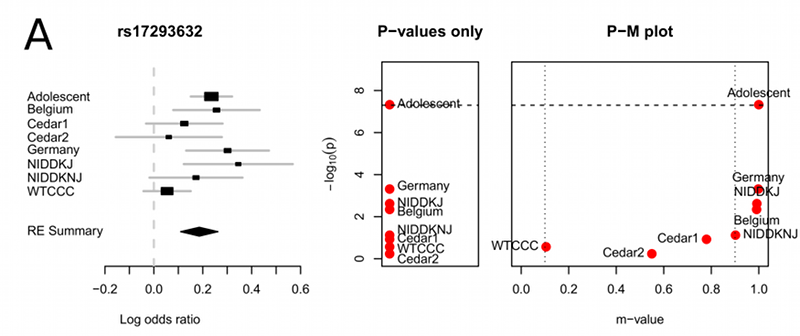
Visualizing heterogeneity in meta-analyses of GWAS. The left panel shows a forest plot which shows the predicted effect size and standard error for each study. The right panel shows a PM-plot which for each study plots the p-value on the y-axis and the m-value on the x-axis. M-values have the following interpretations: Small m-value (e.g. < 0.1) suggest the study does not have an effect. Large m-value (e.g. > 0.9) suggest the study is predicted to have an effect. Otherwise the prediction is ambiguous.
Over the past couple of years, a major focus of our group has been on meta-analysis. These efforts have been led by Buhm Han who is a graduate of our group and now a post-doc at the Broad Institute.
Meta-Analysis is a statistical method to combine the results of many statistical studies. Meta-analysis has the advantage that the statistical power of the combination of the studies is much higher than the statistical power of any individual studies. In fact, the majority of the recently identified genetic variants associated with complex diseases have been discovered using meta-analysis (10.1146/annurev-genom-091212-153520) since most of the effect sizes of these variants are too small to discover in the sample sizes of the individual studies.
Standard meta-analysis techniques assume what is referred to as the “fixed effect model” (FE). In the FE model, the effect size in each study is assumed to the the same. In the case of genetic association studies, this is an unrealistic assumption because the studies are often collected in very different populations which are subject to very different environmental conditions. An alternate model is the “random effects model” (RE) where the effect size are assumed to be different in each study and the effect sizes are modeled as being drawn from a distribution with an estimated mean and variance. This difference in effect sizes between studies is referred to as “heterogeneity.”
Buhm Han, in our group, made two contributions related to heterogeneity in meta-analysis. In his first paper, he noticed that previous approaches for hypothesis testing using the RE model did not correctly model the null hypothesis and led to a significant loss in power(10.1016/j.ajhg.2011.04.014). His second paper presented a method for helping interpret meta-analysis studies to identify in which studies an effect is present and in which studies an effect is not present(10.1371/journal.pgen.1002555). One aspect of the interpretation framework is the m-value which can be used to identify in which studies an effect is present and a summary of the heterogeneity of the meta-analysis can be visualized utilizing a PM-plot (see figure).
The methods are implemented in the software that Buhm developed, METASOFT, available at http://genetics.cs.ucla.edu/meta/.
The full citations to his papers are below:


Pingback: ZarLab · Discovering Genetic Variation that Affects Expression in Multiple Tissues
Pingback: ZarLab · Genes, Environments and Meta-Analysis