Our group recently published a new paper on multiple testing applied to genetic studies with population structure. This project was led by Jong Wha (Joanne) Joo and also involved Farhad Hormozdiari. The project was joint with Buhm Han’s group. The approach built upon Buhm Han’s previous work SLIDE (Han et al. 2009; Han and Eskin 2012).
Genome-wide association studies (GWAS) have discovered many variants that are associated with complex traits in the human genome. In GWAS, researchers collect both phenotypic information and genetic information on variants spread through the genome from a population. In order to identify the set of variants associated with a trait of interest, we assess correlations between the phenotype and the genetic information at each variant, which we call the genotype. GWAS are now routinely performed on tens of thousands of individuals—and millions of genetic variants.
GWAS methodology must address specific problems that are tied to this exceptionally large scale of analysis. One major challenge in GWAS is multiple hypothesis testing. In routine analyses, the significance of hypothesis testing is assessed using the p value as a per-marker threshold. However, GWAS involves computing up to millions of statistical tests in a single study. When using traditional association study techniques, multiple hypothesis testing can generate false positives or spurious associations, and p value threshold for significance must be adjusted to control the overall false positive rate.
Several approaches are useful in correcting these potential pitfalls, including Bonferroni correction and permutation test.
Recently, researchers have accepted the linear mixed model (LMM) as standard practice for performing GWAS. The LMM can address two important challenges in GWAS: population structure and insufficient power. Population structure refers to the complex relatedness structure among individuals, which can drive errors in data reporting such as false positives. In many cases, LMM approaches can increase the statistical power and avoid generating false positives by explicitly modeling the population structure’s genetic relationships. Nonetheless, multiple hypothesis testing with LMM approaches may generate some errors of association. Unfortunately, the current approaches for multiple hypothesis testing correction cannot be applied to LMM. This is because population structure actually affects the correlation structure of the statistics as we show in the paper.
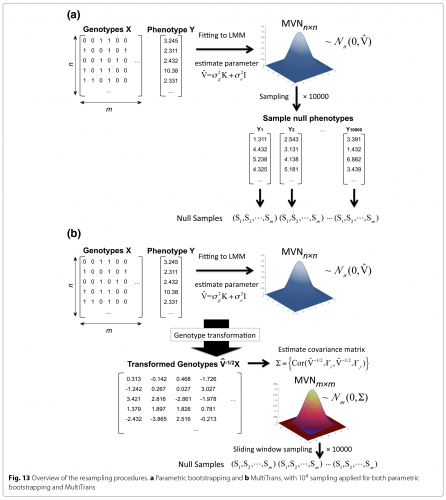
To address this issue, we developed the first gold standard approach for multiple hypothesis testing correction in LMM. This method, called multiple testing in transformed space (MultiTrans), can efficiently correct for multiple testing in LMM approaches. MultiTrans is a parametric bootstrapping resampling approach that is the equivalent of the permutation test. Specifically, our approach samples randomized null phenotypes from the distribution fitted by LMM.
Straightforward parametric bootstrapping where phenotypes are sampled is prohibitively computationally expensive. MultiTrans instead utilizes a Multivariate Normal Distribution to directly samples the association statistics. The figure shows an overview of our methodology.
The full citation to our paper is:
Multiple hypothesis testing is an essential step in GWAS analysis. The correct per-marker threshold differs as a function of species, marker densities, genetic relatedness, and trait heritability—and no previous multiple testing correction methods can comprehensively account for these factors. The method we developed to address this issue, MultiTrans, is an efficient and accurate multiple testing correction approach for LMM. Our method (a) performs a unique transformation of genotype data to account for actual genetic relatedness and heritability under LMM approaches, and (b) efficiently utilizes the multivariate normal distribution. Using MultiTrans, we accurately estimated per-marker thresholds in mouse, yeast, and human datasets—while reducing computation time from months to hours.

